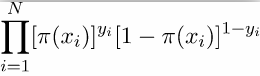本文共 5338 字,大约阅读时间需要 17 分钟。
1、分类、回归、聚类
分类回归是一种重要的机器学习和数据挖掘技术。分类的目的是根据数据集的特点构造一个分类函数或分类模型(也常常称作分类器),该模型能把未知类别的样本映射到给定类别中的一种技术。
即: 向量X=[x1,x2...xn]但标签C=[c1,c2...,ck]的映射F(W,X)=C
聚类是一种无监督学习的方法,将无标签数据聚类到不同的簇中
spark.ml支持的分类与回归算法

2、常见算法实例介绍
2.1、逻辑回归:
2.1.1、逻辑斯蒂分布
2.1.2、二项LR:
![]()
2.1.3、似然函数:
求极大值,得到w的估计值。求极值的方法可以是梯度下降法,梯度上升法等。
from pyspark.sql import SparkSessionfrom pyspark.sql import Row,functionsfrom pyspark.ml.linalg import Vector,Vectorsfrom pyspark.ml.evaluation import MulticlassClassificationEvaluatorfrom pyspark.ml import Pipelinefrom pyspark.ml.feature import IndexToString, StringIndexer, VectorIndexer,HashingTF, Tokenizerfrom pyspark.ml.classification import LogisticRegression,LogisticRegressionModel,BinaryLogisticRegressionSummary, LogisticRegressionspark = SparkSession.builder.master("local").appName("spark ML").getOrCreate()def f(x): rel = {} rel['features'] = Vectors.dense(float(x[0]),float(x[1]),float(x[2]),float(x[3])) rel['label'] = str(x[4]) return rel#读取数据集并转化为DataFrame df= spark.sparkContext.textFile("file:///home/work/jiangshuangyan001/spark_test/iris.txt").map(lambda line: line.split(',')).map(lambda p: Row(**f(p))).toDF()#构建二分数据集df.createOrReplaceTempView("iris")df = spark.sql("select * from iris where label != 'Iris-setosa'")rel = df.rdd.map(lambda t : str(t[1])+":"+str(t[0])).collect()# for item in rel:# print(item)#构建ML的pipelinelabelIndexer = StringIndexer().setInputCol("label").setOutputCol("indexedLabel").fit(df)featureIndexer = VectorIndexer().setInputCol("features").setOutputCol("indexedFeatures").fit(df)df.show()df_train, df_test = df.randomSplit([0.7,0.3])#用setter的方法设置logistic的参数lr = LogisticRegression().setLabelCol("indexedLabel").setFeaturesCol("indexedFeatures").setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8)#print("LogisticRegression parameters:\n" + lr.explainParams())labelConverter = IndexToString().setInputCol("prediction").setOutputCol("predictedLabel").setLabels(labelIndexer.labels)lrPipeline = Pipeline().setStages([labelIndexer, featureIndexer, lr, labelConverter])lrPipelineModel = lrPipeline.fit(df_train)lrPredictions = lrPipelineModel.transform(df_test)#预测结果preRel = lrPredictions.select("predictedLabel", "label", "features", "probability").collect()for item in preRel: print(str(item['label'])+','+str(item['features'])+'-->prob='+str(item['probability'])+',predictedLabel'+str(item['predictedLabel'])) #评估evaluator = MulticlassClassificationEvaluator().setLabelCol("indexedLabel").setPredictionCol("prediction")lrAccuracy = evaluator.evaluate(lrPredictions)print("Test Error = " , str(1.0 - lrAccuracy)) 2.2、决策树
决策树(decision tree)是一种基本的分类与回归方法,这里主要介绍用于分类的决策树。决策树模式呈树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。学习时利用训练数据,根据损失函数最小化的原则建立决策树模型;预测时,对新的数据,利用决策树模型进行分类。
决策树学习通常包括3个步骤:特征选择、决策树的生成和决策树的剪枝。
2.2.1、特征选择
-
信息增益(informational entropy)表示得知某一特征后使得信息的不确定性减少的程度。
![]()
- 信息增益比: 为解决信息增益偏向值多的特征而提出
![]()
![]() 为特征A的熵值
为特征A的熵值
- 基尼指数:分类问题中,假设有K个类,样本点属于第K类的概率为
![]()
2.2.2、决策树的生成
从根结点开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点,再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增均很小或没有特征可以选择为止,最后得到一个决策树。
决策树需要有停止条件来终止其生长的过程。一般来说最低的条件是:当该节点下面的所有记录都属于同一类,或者当所有的记录属性都具有相同的值时。这两种条件是停止决策树的必要条件,也是最低的条件。在实际运用中一般希望决策树提前停止生长,限定叶节点包含的最低数据量,以防止由于过度生长造成的过拟合问题。
2.2.3、决策树的剪枝
决策树生成算法递归地产生决策树,直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确,但对未知的测试数据的分类却没有那么准确,即出现过拟合现象。解决这个问题的办法是考虑决策树的复杂度,对已生成的决策树进行简化,这个过程称为剪枝。
决策树的剪枝往往通过极小化决策树整体的损失函数来实现。一般来说,损失函数可以进行如下的定义:
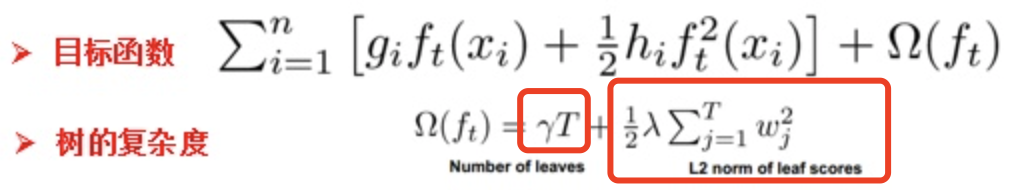
2.2.3、实例
#导入所需要的包from pyspark.ml.classification import DecisionTreeClassificationModel,DecisionTreeClassifierfrom pyspark.ml.evaluation import MulticlassClassificationEvaluator#训练决策树模型,这里我们可以通过setter的方法来设置决策树的参数,也可以用ParamMap来设置(具体的可以查看spark mllib的官网)。具体的可以设置的参数可以通过explainParams()来获取。dtClassifier = DecisionTreeClassifier().setLabelCol("indexedLabel").setFeaturesCol("indexedFeatures")#在pipeline中进行设置pipelinedClassifier = Pipeline().setStages([labelIndexer, featureIndexer, dtClassifier, labelConverter])#训练决策树模型modelClassifier = pipelinedClassifier.fit(df_train)#进行预测predictionsClassifier = modelClassifier.transform(df_test)#查看部分预测的结果predictionsClassifier.select("predictedLabel", "label", "features").show(20)evaluatorClassifier = MulticlassClassificationEvaluator().setLabelCol("indexedLabel").setPredictionCol("prediction").setMetricName("accuracy") accuracy = evaluatorClassifier.evaluate(predictionsClassifier) print("Test Error = " + str(1.0 - accuracy))treeModelClassifier = modelClassifier.stages[2]print("Learned classification tree model:\n" + str(treeModelClassifier.toDebugString)) 2.3、聚类kmeans
1.根据给定的k值,选取k个样本点作为初始划分中心;
2.计算所有样本点到每一个划分中心的距离,并将所有样本点划分到距离最近的划分中心;
3.计算每个划分中样本点的平均值,将其作为新的中心;
from pyspark.sql import Rowfrom pyspark.ml.clustering import KMeans,KMeansModelfrom pyspark.ml.linalg import Vectors#ML包下的KMeans方法也有Seed(随机数种子)、Tol(收敛阈值)、K(簇个数)、MaxIter(最大迭代次数)、initMode(初始化方式)、initStep(KMeans||方法的步数)等参数可供设置kmeansmodel = KMeans().setK(2).setFeaturesCol('features').setPredictionCol('prediction').fit(df)kmeansmodel.transform(df).show()results = kmeansmodel.transform(df).collect()for item in results: print(str(item[0])+' is predcted as cluster'+ str(item[2]))#获取聚类中心的情况#也可以通过KMeansModel类自带的clusterCenters属性获取到模型的所有聚类中心情况:results2 = kmeansmodel.clusterCenters()for item in results2: print(item) #与MLlib下的实现相同,KMeansModel类也提供了计算 集合内误差平方和(Within Set Sum of Squared Error, WSSSE) 的方法来度量聚类的有效性,在真实K值未知的情况下,该值的变化可以作为选取合适K值的一个重要参考:kmeansmodel.computeCost(df) 转载地址:http://mubpz.baihongyu.com/